![\[ x^n = \sum_{t=0}^n S(n,t) \cdot t! \cdot \binom{x}{t} \]](S_1.gif) .
.
A set with an associative binary operation defined upon its elements. There need not be an identity element (as there must be in a monoid), nor is there a requirement that every element must have an inverse (as there is in a group), indeed, without an identity the existance of inverses becomes impossible to define.
A volume contained in a space of specified dimension that has one more boundary point than the number of dimensions, and whose surfaces are defined by linear constraints. A point is a 0-simplex, a line segment is a 1-simplex, a triangle is a 2-simplex, a tetrahedron is a 3-simplex, and so on.
(a) a family of finite sets, closed under subsets.
(b) a collection of simplices meeting face-to-face.
The first type of complex can be made into the second, by embedding the members of the sets in general position in some space of suffiently high dimension, and forming simplices by taking the convex hull of each set. The sets of a simplicial complex are also known as faces.
One of the objects generating a cell of a Voronoi diagram.
The graph formed by the vertices and edges of a polytope or of a cell decomposition of space.
A set of nodes in a graph is called stable if none of them are joined to one another.
A Steiner Triple System of order v is a collection of triples or 3-subsets of a set X of size v such that each pair of elements of X occurs in exactly one triple. In other words a Steiner Triple System is a 2-design with parameters (v, 3, 1, (v-1)/2, v(v-1)/6) . Since the design parameters must be integers, it is necessary that v = 6n + 1 or v = 6n + 3 . Kirkman showed that this is a sufficient condition that a Steiner Triple System exist.
The Stirling numbers of the second kind, S(n,t), have the combinatorial interpretation of counting the number of ways of partitioning an n element set into t non-empty subsets. Given the finite difference table for the monomial xn the Stirling numbers of the second kind can be derived from the differences at zero by dividing the t-th difference by t factorial. Thus we have the following equation for xn:
![\[ x^n = \sum_{t=0}^n S(n,t) \cdot t! \cdot \binom{x}{t} \]](S_1.gif) .
.
The Stirling numbers of the second kind satisfy a recurrence relation:
S(n,t) = t*S(n-1,t) + S(n-1,t-1)
The Stirling numbers of the first kind, s(n,t), are the
coefficients on the monomials in an expansion of polynomials
of the form
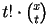 .
.
The Stirling numbers of the first kind satisfy the recurrence formula s(n,t) = s(n-1,t-1) - (n-1)*s(n-1,t)
with initial values, s(n,0) = 0 for n = 1,2,3,... and s(n,n) = 1 for n = 0,1,2,3,...
A design in which the parameters (v, k, lambda, r, b) are such that v = b and k = r .
Given a set S and a family of subsets A1, A2, ... Ak of S, a System of Distinct Representatives is an assignment of k distinct elements s1, s2, ... sk of S such that si is in Ai for all i.