The nerve of the cells of a Voronoi diagram. The Delaunay triangulation corresponding to a Voronoi diagram in R2 is its planar dual. For point sites in general position, the Delaunay triangulation is a triangulation of the sites' convex hull.
A permutation with no fixed points. In other words a rearrangement of an ordered set of things so that no element is in its original position.
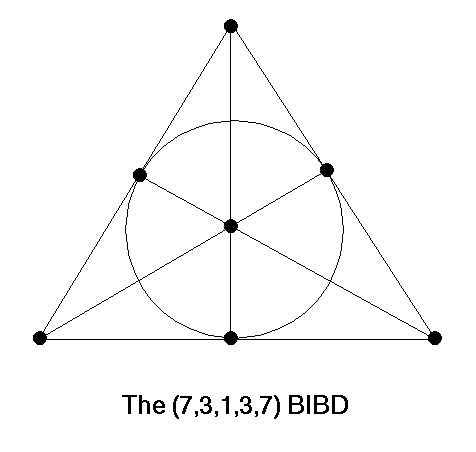
A design or BIBD (Balanced Incomplete Block Design) with parameters (v, k, lambda, r, b) is an incidence system (the name 'Design' comes from the original use of these combinatorial structures in the design of industrial and agricultural experiments) in which a set of v 'points' is partitioned into b 'blocks' in such a way that any two points determine lamda blocks. There are k points in every block, and each point is contained in r different blocks. In a more general form, a t-Design (with t > 2) has the property that any t points determine lambda blocks.
The prototypical example of a design is the projective space of dimension 2 over GF(2) aka the Fano plane, which is a design with parameters (v=7, k=3, lambda=1, r=3 and b=7) this is also an example of a symmetric design and a Steiner triple system
The maximum distance between any two points in a set.
A subset of the elements of a group (written additively) with the property that if
a table of all of the differences x-y (with x and y
in the distinguished
subset) is made, every non-identity element of the group occurs in this
table the same number of times. The quadratic residues in GF(11)
form a
difference set. Suppose that there is a difference set of size k
in a group G,
then twice the binomial coefficient
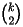must be a multiple of |G|-1.
A Digraph or directed graph is a graph in which the edges have an explicit direction, thus the set of edges becomes a set of ordered pairs.
Also known as a skew field. A ring in which every non-zero element has a multiplicative inverse, a division ring lacks only commutativity or it would be a field.
The quaternions are a good example of a division ring.