Suppose we receive the word (000000000001100000101111) over a noisy channel, we see immediately (because this word's Hamming weight is 7 -- not 0,8,12,16 or 24) that some errors have occured in transmission.
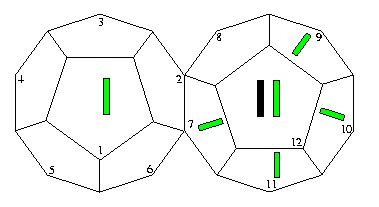
We first write this word on the surface of a dodecahedron. We use a black pen to write the first 12 bits, one on each face, and a green pen to write the second 12 bits.
The result is:

Next we make our twelve decoding checks, and we mark the faces for which the decoding checks failed.
In the case above, the resulting pattern of failed decoding checks is:
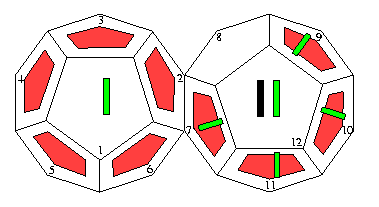
Which of the nine patterns that we have considered is this? (Don't forget that some of the the patterns must be recognized with 1 or 2 modifications.)
We can be somewhat systematic. There are 9 failed decoding checks in the above example, recall that the weights of the 9 patterns we looked at in the previous section are:
The only patterns that (unmodified) have weight 9 are the "Deep Bowl" and the "Cage". The pattern we have here is neither of these. The "Diaper" and "Bent Ring" patterns would need 3 additional faces to become weight 9, but they already represent patterns of 2 errors in information positions, thus we would be talking about 5 errors if we tried to make these fit the given pattern.
The remaining possibilities are a "Parachute" with 2 additional faces or a "Tropics" with 1 face removed. A "Parachute" augmented with 2 faces could never have a pair of opposite faces in its complement so we must have the latter.
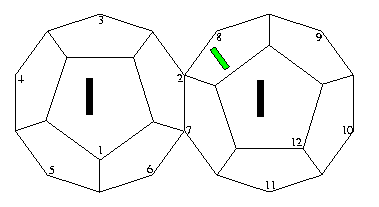
Returning to the diagram for "Tropics", we see that the 2 information bit errors occured in the 2 opposite missing faces (1 and 12) and the additional missing face (8) corresponds to a parity check error in that position.
The error vector is:
Thus the original vector that was transmitted must have been:
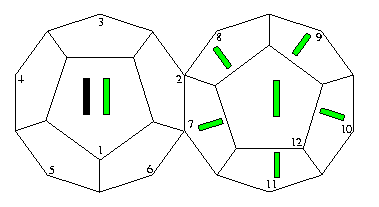
It should be easy to recognize this vector as the result of encoding when a single information bit in the first coordinate is set.