In this section, we describe the process of decoding.
Recall that the minimum Hamming distance between any two codewords in the Golay code is 8. This means that if a codeword is altered (for instance during transmission through a noisy communication channel) in 3 or fewer positions, it will still be closer in Hamming distance to the original codeword than to any other. It should also be noted that if 4 alterations are made, it is possible (in fact inevitable) that the modified word will be equally close to two or more codewords.
Our job in decoding is to find the 12 information bits that correspond to the originally transmitted codeword from an altered version of that codeword. We will only be interested in correcting patterns of 3 or fewer errors -- if 4 errors have been introduced, we will be able to detect the situation, but not correct them. If 5 or more errors are introduced, we will (unfortunately) decode incorrectly.
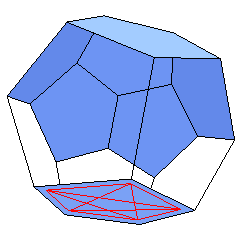
Our decoding process will consist of making 12 so-called decoding checks -- one for each face of the dodecahedron. We will say a decoding check fails if the result is 1, and that it passes if the result is 0. We then consider the decoding checks as giving a partial dodecahedron, a face will only be present if the corresponding decoding check failed. Finally, we will have to look at this partial dodecahedron and distinguish it as one of roughly 9 possibilities. (It is at this point that we rely on human pattern recognition.)
A decoding check is made in very nearly the same way as a parity check. We place the mask over each face of the dodecahedron and count the parity of the information positions that are visible outside of it, we then add the parity check symbol that is visible in the center of the mask. If this parity (counting 7 information positions and a single parity position) is even, the decoding check has passed, if odd, it has failed.
Clearly, if no errors at all are introduced, all of the decoding checks will pass.
Consider what will happen if a single error is made in transmission. If that error is in a parity check symbol, it will only effect the decoding checks one time, namely, when the mask is centered on the corresponding face. Thus our partial dodecahedron will be very partial indeed, consisting of just a single face! If the error happens to be in an information symbol, the decoding checks will pass whenever the mask is placed so that that face is covered -- i.e. when it is centered on the faces adjacent to the error position. In that case, we will get the complement of our mask as the partial dodecahedron, a figure I call the "Parachute". The error actually has occurred where the "skydiver" sits.
In the images and VRML models that follow, the error positions are indicated with red stars. These may or may not conincide with sites where the decoding checks failed (which are indicated by coloring the corresponding face blue).
What if 2 or 3 errors are introduced? We will first consider the possibility (mostly to dispose of it quickly!) that the errors are in parity check symbols. If that is the case we will simply have a partial dodecahedron consisting of 2 or 3 pentagons, and we will know that parity check symbol errors have occurred in those same positions.
Suppose that a single information position is in error, and additionally, one or two of the parity symbols are also wrong. In this situation, we will need to be able to recognize the "Parachute" with some holes in it, or extra faces tacked on.
If two errors have occured in information positions, there are three cases to consider:
The partial dodecahedra represented by the failed decoding checks are called (respectively):
These 3 configurations could also be accompanied by at most 1 error in a parity check symbol; therefore we will need to be able to recognize them with a single hole, or an extra face tacked on.
Finally, we turn to the possibility that 3 errors have all occurred in information positions. In this situation, there are exacly 5 configurations to consider. These correspond to the 5 "triangles" that can occur on the dodecahedron. By a triangle, we simply mean a collection of 3 faces. For example, if we have 3 mutually adjacent faces, they correspond to a triangle having side lengths (1,1,1).
We leave it to the reader to verify that the five possible triangles have side lengths:
The partial dodecahedra for these error patterns are: