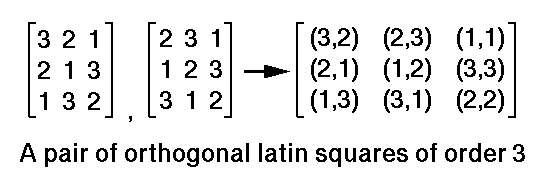
A Latin Square of order n is an nxn array made from the integers 1 to n with the property that any integer occurs once in each row and column.
A pair of Latin squares are called orthogonal if the n-squared pairs formed by juxtaposing the two arrays are all distinct.
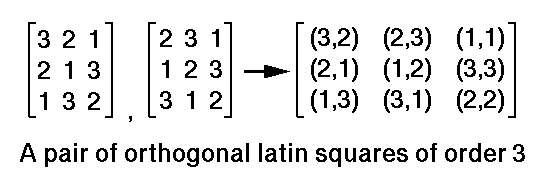
A subset of real or complex (or quaternionic) n-space that consists of all finite sums of a set of n independent generating vectors with coefficients in the corresponding ring of integers.
An algebraic system generalizing the notion of unions and intersections of sets.
A lattice (in the sense of def. 1) that is built up in layers. One takes an n-dimensional lattice, and in n+1-dimensional space place copies of it next to one another so as to build up an n+1-dimensional lattice. The vectors that determine how succeeding layers lie next to one another are called "glue vectors".
The lattice that is used to store cannonballs, (and to display fruit) is a laminated lattice built up out of successive layers of the hexagonal close packing.