The animated sequence below illustrates a proof of the Pythagorean Theorem:

where X and Y are the shorter sides of a right triangle, and Z is the long side.

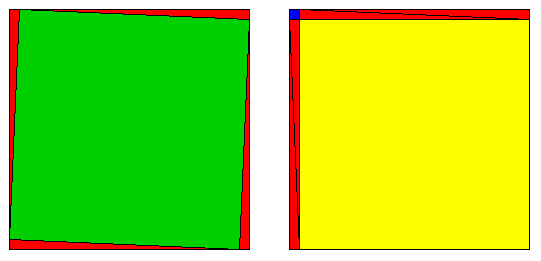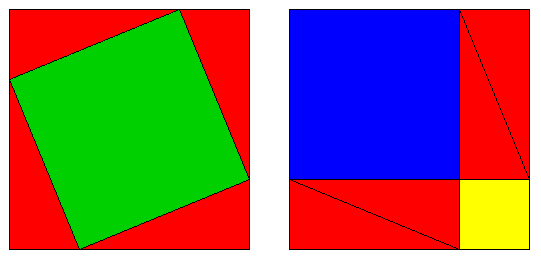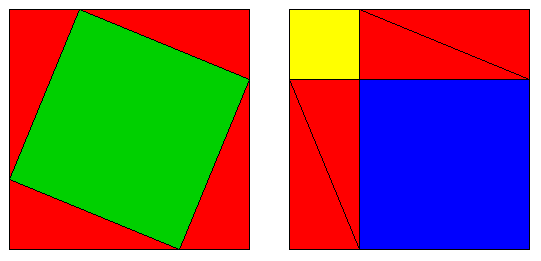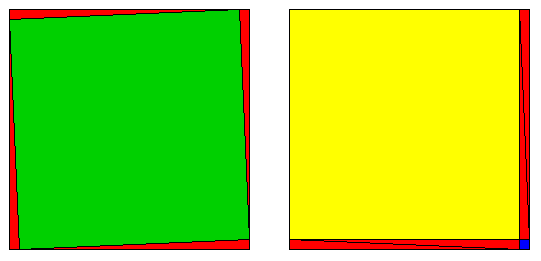
Any single frame of this animation contains two pictures of the same square. One square has four red triangles arranged in it so that the left-over area is the square of their hypotenuse(s). The other square has them arranged so that the remaining area is the sum of the squares built on the other two sides.

The animation just shows that the argument is general, i.e. that it doesn't depend on the properties of some particular triangle.