A Small Puzzle

I call the following visual proof that the sum of the first n consecutive odd numbers is n², the "L"-decomposition.

Suppose we have two "L"-decompositions, can the pieces of these two decompositions be reassembled into a single larger square?

Well, clearly it is necessary that the two "L"-decompositions we start with are part of a Pythagorean triple. (A triple of integers that satisfy the Pythagorean formula, for example (3,4,5) or (5,12,13).)

In the case of the Pythagorean triple (3,4,5), a solution is given below.

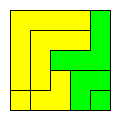
For every Pythagorean triple that I have tried, eventually a solution was found. There is no reason whatsoever why this should always be possible! But that is what seems to be the case!

Here is the solution for the (5,12,13) Pythagorean triple.

Update: Jan. 13, 1998

Erich Friedman has conjectured that every sum of squares (i.e. things like 7² + 7² + 1² + 1² = 10²) works this way. He has also described proofs that there are infinite families of solutions that can be generated recursively.

The smallest triple that no one has found a solution for is (20,21,29).